Interval Analysis and its Applications to Optimization in Behavioural Ecology
Researcher: Justin Tung (jt96@cornell.edu)
Instructor: David Schwartz
(dis@cs.cornell.edu)
Contents:
Overview
Paper
Software
Overview
1. Abstract
Interval Analysis is a means of representing uncertainty by replacing single
(fixed-point) values with intervals. In this project, interval analysis is
applied to a foraging model in behavioural ecology. The model describes an
individual foraging in a collection of continuously renewing resource patches.
This model is used to determine the optimal residence time of the forager in a
resource patch assuming the forager wants to maximize its rate of resource
intake. Before applying interval analysis, fixed-point (non-interval)
optimization will be done to serve as a basis. Certain parameters in the mode
will then be replaced with intervals and interval-based optimization conducted.
A comparison of the interval and fixed-point results will be done as well as
analysis of parameter intervals and their constraints, root approximations, and
applications to the model.
Key Words: single variable optimization, interval analysis,
behavioural ecology, foraging
The paper covers only a brief outline of Interval Analysis (IA) and the math associated with IA that is needed to understand the topics covered and assumes some prior knowledge of IA and Matlab though it is possible to understand the applications to the foraging model without that knowledge. For a formal mathematical introduction and in depth coverage of concepts see Schwartz (1999) or Moore (1966) listed in the references. Interval analysis is a deterministic way of representing uncertainty in values by replacing a number with a range of values (Schwartz 17). Fixed-point analysis is simply analysis using non-interval values where there is no uncertainty in the values. As a result, IA uncertainty concepts can be used to model varying biological parameters in the ecological model and also to frame fixed-point results. One website providing an excellent gateway to interval analysis resources and information is at http://www.cs.utep.edu/interval-comp/main.html
3. Behavioural Ecology and the Foraging Model
Foraging models in general study two basic problems of a forager: which food/prey items to consume and when to leave an area containing food (a resource patch). This paper will concentrate on the latter as an optimization problem. The paper discusses the framework of foraging models and also explains foraging and optimality models through the three main components of decision, currency, and constraint assumptions. Given the structure of a foraging model, it is easy to frame a model examining the foraging of a single animal over a collection of distinct resource patches. I have taken the model along with its decision, currency, and constraint assumptions from Wilson (2000) (in references) so the construction of the model's equations, its origins, and an analysis and extensions of the model in C can be found in his book. The rules of the forager in the model are that the animal stays for a fixed time before moving to a new resource patch, time is discrete, and patch resource values (biomass, energy, etc) grow logistically. The decision assumption lies in the determination of the fixed time value. Assuming behavioural and evolutionary mechanisms drive foragers to optimize the time spent on each patch. This assumption implies that they will stay long enough to optimize the rate of resource consumption.
The mathematical conclusion, explained in the paper using the model's structure is that the optimal time to leave a patch is when the expected rate of resource return decreases to the average rate of return of a new patch (a statement of the marginal value theorem for foraging). This result then allows an optimization problem to be constructed.
4. Methodology
The optimization problem was approached in two ways. One way was a fixed point
analysis of the problem using the bisection method after some
graphical analysis of the functions involved. The second way was an IA
approach using the interval Newton's method. The results and details
of these two methods and their comparisons can be found in the paper. A
stability analysis was also conducted on the model, which was
testing the limits of the uncertainties of the variables before the model
"broke down".
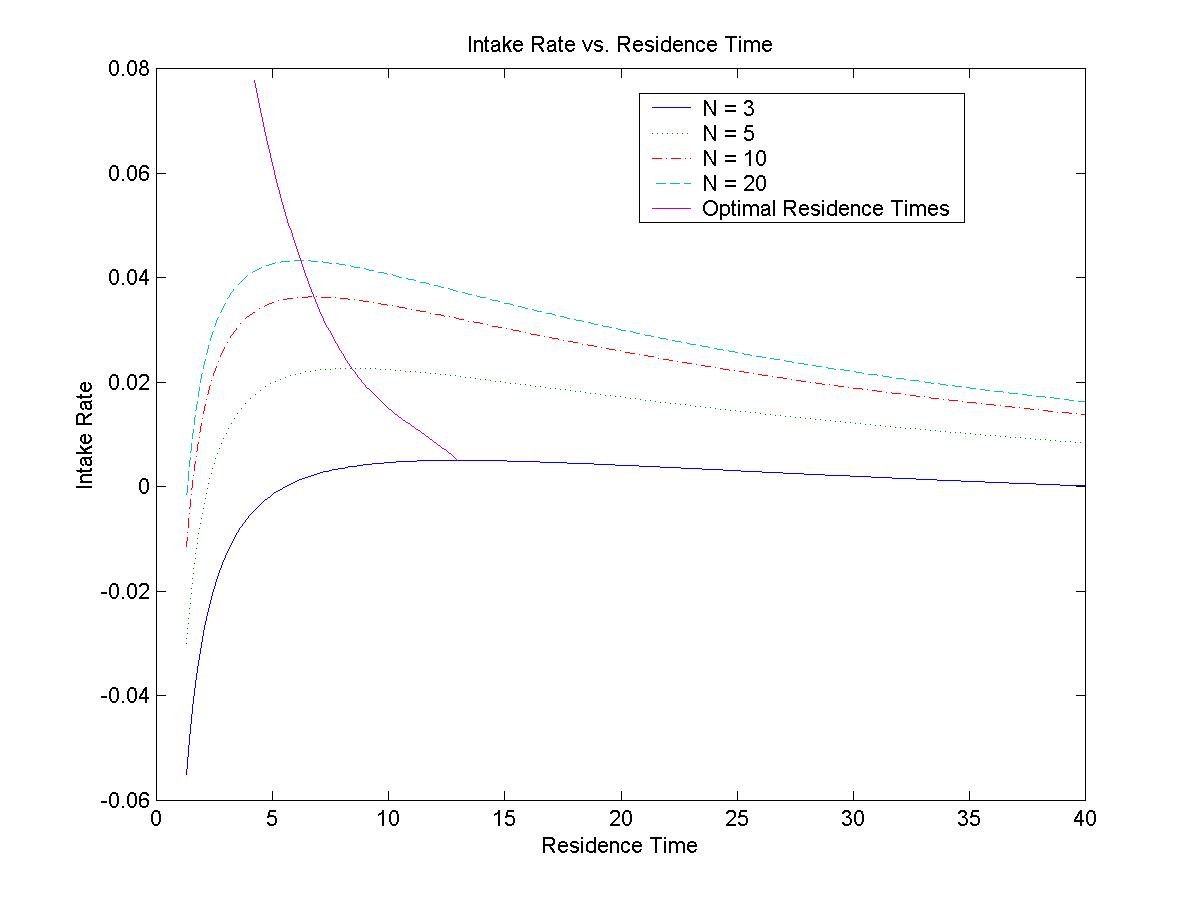
5. Summary Results
The values obtained from both optimization methods corresponded well
since error bounds derived from the error between the fixed-point roots and
the endpoints of the optimal residence time intervals shows relatively small
differences from each other. The use of IA to simulate a range of parameter
states in the system was successful since the percent uncertainties yielded
interval optimal residence times. As a result, IA allows the ecologist to
vary parameters of the model within certain limitations established by
stability analysis and obtain a range of optimal residence times a forager
might choose. The percent uncertainty limitations on parameter variation
obtained from the stability analysis are high, which is good since it allows
a large amount of model variability.
IA's applications to the foraging model include adding more realism to the model through deterministic variability as well as allowing the ecologist to select which parameters are to be uncertain, their range, or different beginning time intervals. The variability is important due to the stochastic nature of ecological process and IA offers an alternative to average state approximations.
Paper
Interval Analysis and its Applications to Optimization in Behavioural Ecology
January 2002
Report
See the paper regarding descriptions and functions contained in this site
(version 1.0). The site contains all
the m-files (matlab files) listed below:
| Text User Interface | Support Functions | Data Analysis | Numerical Algorithms |
|
main.m dispara.m disparafp.m disparaia.m fpOptimizeMain.m intOptimizeMain.m selectP.m selectPIA.m |
gain.m gainPrime.m gawMax.m newInterval r.m rootFunc.m rootPrime.m |
sa.m ga.m fpOptimize.m intOptimize.m |
bisection.m intNewton.m UnitedNewtonStep.m |
II. Project Files
The language used in this project was Matlab version 5.3 with an add-on
toolbox called INTLAB programmed by Siegfried Rump (2001). Refer to
http://www.ti3.tu-harburg.de/~rump/intlab/index.html for
additional information on the INTLAB toolbox. For this paper, the INTLAB toolbox
was used to provide interval data structures, implementation of interval
arithmetic and interval-valued functions, as well as basic functions for radius,
midpoint, and intersection interval functions in Matlab.
References
Hart, John C. "Ray Tracing Implicit Surfaces." Notes for Advanced
Surface Modeling.
http://graphics.cs.uiuc.edu/~jch/cs497jch/rtis.pdf (8 Nov. 2001).
Hansen, E. R. "Global Optimization Using Interval Analysis: The One-Dimensiona
Case" Journal of Optimization Theory and Applications
29 (1979): 331-344.
Krebs, John R. and N. B. Davies. An Introduction to Behavioural Ecology.
2nd ed. Sunderland: Sinauer Associates, Inc., 1987.
Kulisch, U., R. Lohner, and A. Facius., eds. Perspectives on Enclosure
Methods. New York: Springer-Verlag, 2001.
Moore, Ramon E. Interval Analysis. Englewood Cliffs: Prentice-Hall,
Inc. 1966.
Neumaier, Arnold. Interval Methods for Systems of Equations.
New York: Cambridge University Press, 1990.
Rice, John R. Numerical Methods, Software, and Analysis.
2nd ed. New York: Academic Press, Inc., 1993.
Rump, Siegfried M. "INTerval LABoratory Version 3." INTLAB
http://www.ti3.tu-harburg.de/~rump/intlab/index.html
(14 Dec. 2001).
Schwartz, David I. Deterministic Interval Uncertainty Methods for
Structural Analysis. Diss. State University of New York at Buffalo,
1999.
Stephens, David W. and John R, Krebs. Foraging Theory.
Princeton: Princeton University Press, 1986).
Van Loan, Charles. Introduction to Scientific Computing.
2nd ed. Upper Saddle River: Prentice Hall 2000.
Wilson, Will. Simulating Ecological and Evolutionary Systems in C.
Cambridge: Cambridge University Press, 2000.
ARTEMIS | resources/cs490/cs490.html by justin tung generated using Apache Software Foundation's Xalan-J version 2.7.2
